t검정(t-test)
평균 분산 표준편차 왜도 첨도 중앙치 최빈치 등등 기본적인 통계학적 개념을 떼고나면 제일 처음 배우는 검정이 바로 t검정이다.(z검정일 수도 있다.) t검정의 기본논리는 2개의 평균이 서로 유의하게 차이가 있느냐 없느냐를 알아보는데 있다. t검정을 사용하는데 있어 다음과 같은 가정을 필요로한다. 첫 째, 구간, 비율척도를 사용해야한다. 둘 째, 분산의 동질성 가정을 충족시켜야한다. z검정의 경우, 모집단의 분산과 표준편차를 알아야하지만, t검정은 몰라도 사용이 가능하다. 여담으로 t검정이지 T검정이 아니다. 이상하게도 spss 한글판에서는 T검정으로 번역되었다.
1. 단일표본 t검정 (One Sample t-test)
단일 표본이 특정 기준값(모집단 평균)과 유의미하게 다른지 검정할 때 사용한다. 예시를 들어보자. 당신은 어느 대학의 학사지원팀에서 학업 성취도 요건을 확인하는 담당자이다. 당신은 보고서를 쓰다가 어떤 생각이 문득 떠오른다. 과연 우리 학교 학생의 토익점수는 전국 대학생 평균 토익 점수와 유의미하게 차이가 있을까?

한국인의 평균 토익 점수가 2024년 기준 709점인 것으로 나타났다. 그렇다면 귀무가설과 대립가설을 다음과같이 설정할 수 있다.
H0 : 우리 대학교 학생의 토익의 점수는709점과 차이가 없다. μ = 709
H1 : 우리 대학교 학생의 토익의 점수는709점과 차이가 있을 것이다. μ ≠ 709
다음은 spss에서 단일표본검정의 절차이다.

분석(A) - 평균비교(M) - 일표본 t검정(S)에 들어간다.

왼쪽에 있는 토익점수를 오른쪽으로 옮기고, 비교하려고하는 점수는 전국의 토익점수 평균인 709점이니, 검정값(V)을 709로 설정하고 확인을 누른다.

그럼 다음과 같은 값이 나온다. 일표본 통계량에서 N은 표본이다. 300명에 대한 값을 뜻하고, 평균에서 618.28이 나왔다. 즉, 학교에서 토익에 응시한 300명의 평균이 618.28점이 나왔다는 것이다. 표준편차는 알다시피 데이터가 평균을 중심으로 얼마나 퍼져 있는지를 나타내는 지표다. 대학 내의 대부분 학생의 점수는 (618.28 ± 76.923) 범위이며 정규분포 상에서 약 541점에서 695점 사이에 위치할 가능성이 높다는 의미다.
두 번째로, 일표본 검정에서 t는 -20.426이 나왔다. 해당 예시에서는 표본 평균(618.28)과 검정값(709) 간의 차이가 통계적으로 유의한지 나타내는 값이며, 음수가 나왔다는 것은 표본 평균이 검정값보다 낮음을 의미한다. 자유도는 N-1이므로, 299가 나타났다. 평균차는 교내의 학생의 평균과 전국의 토익평균의 점수를 비교한 값이고, 90.717의 차이가 나타났다.
유의확률값이 0.05보다 작으므로, 귀무가설인, "우리 학교 학생들의 평균 점수는 709점과 차이가 없다" 에 대한 가설을 기각할 수 있다. 즉, 우리 학교 학생들의 평균 토익 점수(618.28점)는 전국 평균(709점)보다 유의하게 낮다는 것을 보여준다.
2. 독립표본 t검정 (Independent Samples t-test)
심리학 연구에 있어, 실험집단과 통제집단으로 나누어서 집단 간의 동질성 검증을 위해 주로 사용된다. 예를 들면, 연령대, 소득수준, 교육, 근무시간, 혈압같은 연속형 변수에 대해서 사용한다. 성별의 경우 이분변수이므로 카이제곱검정으로 비교해야한다. 동질성검증도 가능하지만, 집단 간의 차이가 있는지에 대해서도 알 수 있다. 예를 들면, 통제집단과 실험집단의 치료처치 효과에서 차이가 나는지 나지않는지를 척도를 통해 비교할 수 있다.
1). 동질성 검증
동질성이 확보되어야 실험 결과가 처치의 영향으로 발생했다는 근거로, 우울증 완화 프로그램 효과를 검증하려고하는데 있어, 실험집단과 통제집단, 집단 간의 동질성을 검증하고자한다. 나이, 혈압, 초기우울점수가 동질성검증에 있어 변인의 예시가 될 수 있을 것이다. 중요한 것은 한 번에 검정을 못하고, 각 변인에 대해 각각 검정을 해야하니까 3번의 과정을 거쳐야한다.
2). 집단 간의 차이비교
당신이 외상 후 울분장애 성향을 가진 중년 남성을 대상으로 치료의 효과를 검증하려고 한다. 여기에서 외상후 성장 척도(K-PTGI-X)를 사용하여 실험집단과 통제집단의 점수의 차이를 비교하는 것이 예시가 될 수 있을 것이다.
다음 독립표본 t검정의 예시를 2) 집단 간의 차이비교로 spss에서 검정절차를 알아보겠다.

분석(A)-평균 비교(M)-독립표본 t검정(T)로 들어간다.

집단변수에는 그룹을 넣고, 검정변수에는 외상후성장에 대한 값을 넣는다.

집단정의(D)를 누르면 이름을 설정할 수 있다. 집단1은 실험집단, 집단 2는 통제집단이다. 설정 후, 계속-확인을 클릭한다.

다음과 같이 결과값이 나온다. Levene의 등분산검정에서 유의확률 값이 .576으로 유의수준 .05보다 크므로, 귀무가설을 기각한다. 즉, 등분산이 가정되었다는 것이다. 그룹1의 평균은 76.68, 그룹 2의 평균은 60.14다. 유의확률에서는 .000이 나왔으므로, 해당 집단 간의 차이는 통계적으로 유의하다고 볼 수 있다.
3) 대응표본 t검정(Paired t-test)
두 조건이나 두 시점 간의 평균 차이를 비교할 때 사용하는 통계 기법이다. 이 검정의 가정은, 두 데이터가 서로 대응되어 있다는 것을 가정한다. 즉, 집단 간의 비교가 아니라, 같은 집단을 비교하는데 적합하다는 것이다. 만약 집단 간의 차이를 검증하고자 한다면, 독립 표본 t-검정 또는 ANOVA 같은 다른 통계 기법을 사용하는 것이 더 적절하다.
예를 들어보자. 당신은 마음챙김 훈련프로그램의 효과성을 검증하기위해 전 후로, 참가자의 스트레스지수의 변화를 측정하고자 한다. 훈련 전에 한 번, 훈련 후에 한 번씩 짝지어서 검정하는 것이 대응표본 t검정인 것이다. spss의 검정을 통해 예시를 들어보도록하겠다.
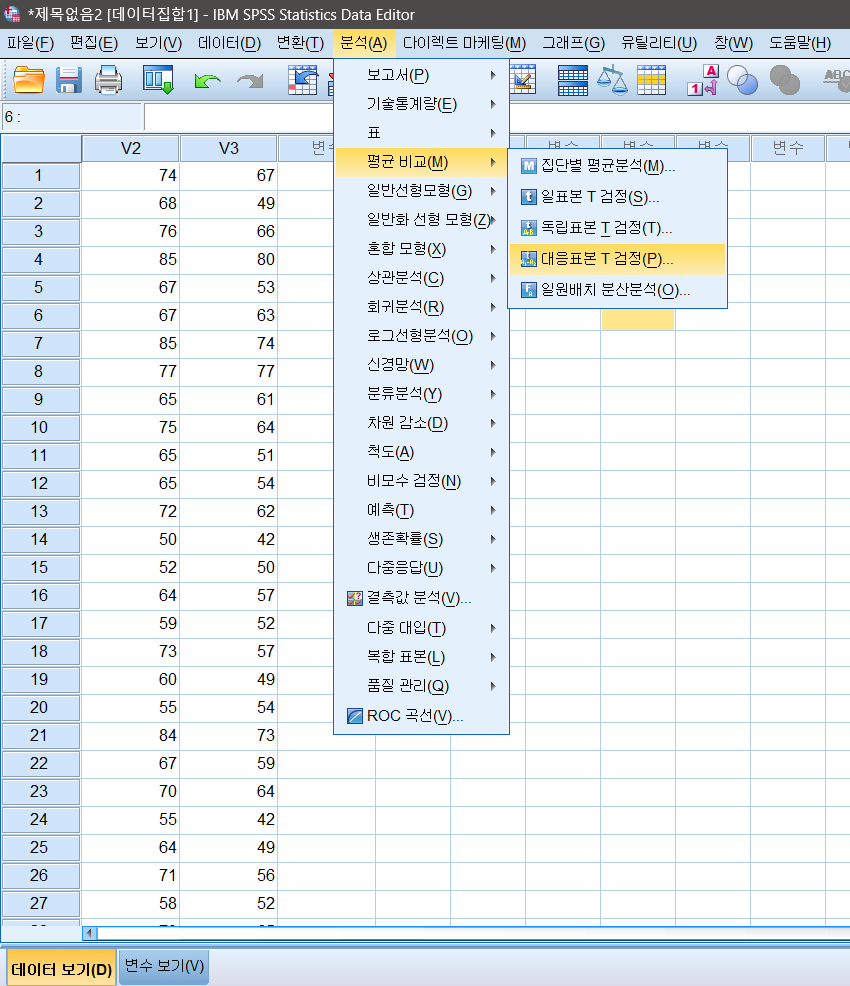
분석(A) - 평균비교(M) - 대응표본 t검정(P) 를 클릭한다.

대응할 변수에 대해 다음과 같이 드래그하고, 확인을 누른다.

다음과 같은 화면이 뜬다. 당연한 이야기지만, 한 집단의 대응표본이기때문에, 표본의 수는 각각 모두 같아야한다.
V2는 사전의 점수, V3는 프로그램 후의 스트레스 점수다. V3(사후) 점수가 V2(사전) 점수보다 낮아졌으며, 이는 평균적으로 약 9.33점 차이가 있음을 알려주고 있다. 상관계수가 0.877으로 두 변수(V2와 V3)는 높은 상관성을 보이고 있다. 이는 동일한 참가자에서 두 측정치가 밀접하게 관련되어있음을 뜻한다. 상관계수와 대응표본 검정의 유의확률이 모두 0.00으로 유의수준 0.05보다 낮으므로 통계검정이 유의하다고 볼 수 있다.
z검정(z-test)은 심리학 연구에서는 거의 사용되지않기에 생략하도록하겠다. 연구를 하려고하는 모집단의 분산(σ²)과 표준편차(σ)를 파악하기가 어렵기 때문이다. 논리는 t검정과 유사하니 생략하도록한다. 다만 이런 차이점이 있다는 것을 알아만두면 될 것이다.
해당 예시의 데이터파일이다.