마할라노비스 거리(Mahalanobis distance)
인도 통계학의 아버지, Prasanta Chandra Mahalanobis가 1936년에 발표하였다. Mahalanobis distance보다 대규모 표본조사의 방법론을 집대성했다는 것이 더 유명하다. 여담이지만, 인류학 연구에서 두개골 측정값을 이용한 유사성 분석을 하다가 발명되었다.

그래프를 통해서 Mahalanobis distance의 논리를 알아보자.

대다수의 데이터는 공분산 구조를 고려한 다변량 정규 분포를 따를 때, Normal Data는 위의 그림과 같이 고르게 분포되어있다. 그러나 그렇지 않은 데이터도 있다. 빨간색 점에서 데이터가 분포되는 경우는 이상치(Outliers)에 속한다고 볼 수 있다. 즉, 특정 점이 분포의 중심에서 얼마나 벗어나 있는지를 평가하는데 목적을 둔다.

문제는 데이터가 다변량 정규성을 가정하지 않는다면 이상점 기준을 잡을 수 없기 때문에 마할라노비스 거리를 사용할 수 없다.

어디서 많이 본 논리이지 않은가? 그렇다. 표준정규분포에서 볼 수 있는 개념과 유사하다. 표준정규분포에서도 중심에서 멀어질수록 표준편차가 증가하며, 데이터가 해당 범위 내에서 관측될 확률이 낮아진다.
당신이 연구에서 척도지를 사용했다면, 정규분포의 논리상 누군가는 불성실한 응답을 할 것이다. 선행연구마다 불성실응답의 비율은 상이하지만, 보통은 10% 내외로 나타난다. 문제는 이게 통계분석을 하는데 있어서 타당도를 심각하게 저해한다는 것이다. Crede (2010)에 의하면, 표본의 5~10%의 응답자가 불성실하게 답했다면 심리적 측정의 속성이 심각하게 달라진다고 한다. 그렇기에 연구자는 불성실한 응답을 찾아 제거해야만 연구의 타당도를 높일 수 있을 것이다.
보통 심리학 연구에서는 정규성 가정이 필요 없는 사분위범위를 사용하여 이상치를 제거한다. 그러나 개별문항만을 고려해서 이상치를 찾아내기에 다변량을 고려하지 못한다. 즉, 여러 변수간의 관계를 반영하지 못한다는 단점이 있다. 그외에 롱스트링방법이나, FMM도 있지만, 롱스트링은 정밀하게 파악하지는 못하고, FMM은 유료 프로그램인 Mplus를 사용해야한다. R로 무료로 사용할 수 있지만, 코딩 작업이 너무 어렵다.(코드 하나만 틀려도 분석을 안 해준다..) jamovi도 R을 깔아서 수행해야한다. 결국 기본적인 분석을 제공해주는 SPSS를 사용한 Mahalanobis distance를 사용하는 것이 제일 간편하다.
Mahalanobis distance는 다변량 정규분포를 가정하며, 연구에 사용되는 변수들 간의 공분산을 고려하여 분석을 수행해야 한다. 따라서, 변수 간 상관성이 지나치게 낮다면 유의한 결과를 얻기 어려울 수 있으며, 공분산을 반영하는 분석 특성상 지나치게 독립적인 척도들(상관성이 거의 없는 경우)에서는 적용하기 힘들다는 단점이 있다.
Mahalanobis distance가 사용된 연구는 외상 후 성장 척도 확장판(PTGI-X)의 심리측정적 속성: 한국판 척도의 요인구조와 유용성 재검토(임선영 2023)가 있다. 이 연구에서 PTGI-X 25개 문항에 대해 Mahalanobis distance (D) 제곱값을 계산한 후, χ² 분포의 상위 5% 백분위(DeSimone & Harms, 2018)를 초과하는 27개의 자료를 정규성에서 과도하게 벗어난 이상치로 간주하고 분석에서 제외하였다.
요인분석에서는 측정 변수(문항)들 간의 공분산(Covariance)을 이용하여 공통 요인(Common Factors)을 추출한다. 그러나 극단적으로 다른 응답을 한 이상치가 존재하면, 공분산 행렬이 왜곡되어 요인분석 결과가 부정확해질 수 있다. 그렇기에 Mahalanobis distance 방법을 사용한다면, 변수 간의 관계(공분산 행렬)를 고려하여 다변량 이상치를 탐지할 수 있고, 요인분석 전에 이상치를 제거하는 데 적합하다.
SPSS를 통해 어떻게 Mahalanobis distance를 통해 이상치를 탐색할 수 있는지 알아보자.
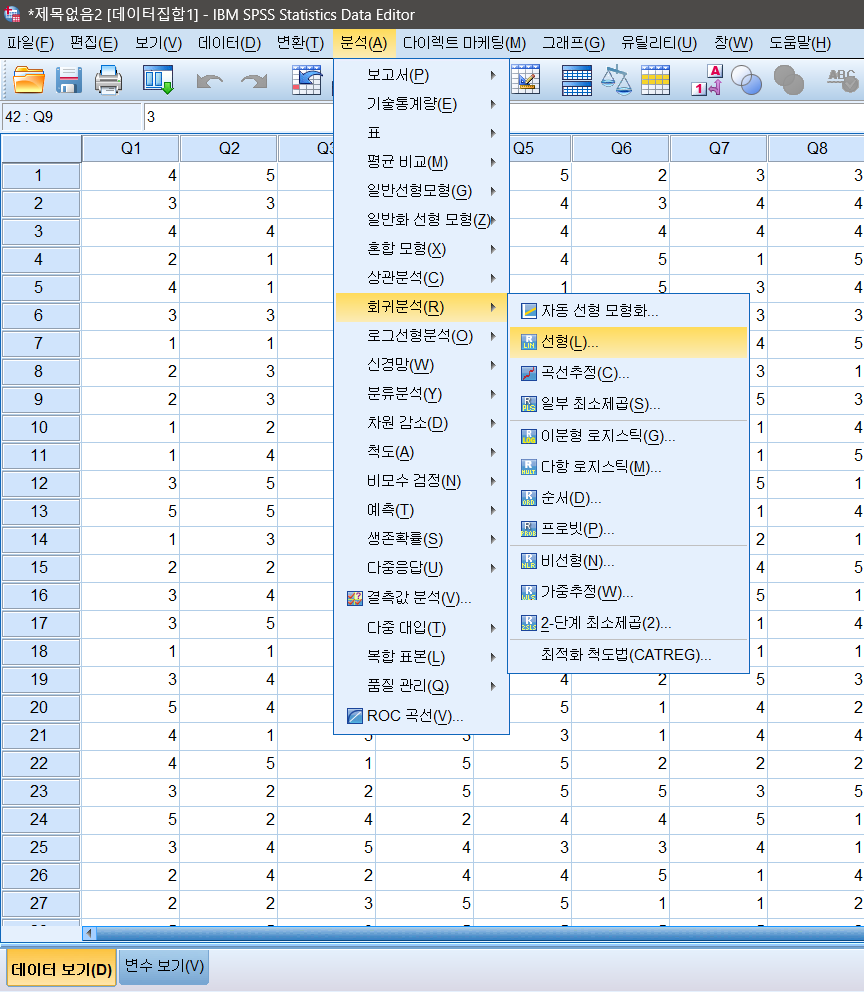
분석(A) - 회귀분석(R) - 선형(L) 을 클릭한다.

예시로 25문항의 척도지를 사용했다. (단일 문항이 아닌 여러 속성을 측정하는 척도의 문항 합이 25개라고 가정한다.) 종속변수의 Q1을 넣고 나머지 독립변수에 Q2~25를 채워넣는다. 단순 계산용으로 사용되기때문에 순서는 상관없다. 그 후, 저장(S)를 클릭한다.

다음과 같이 Mahalanobis distance가 있는 것을 확인할 수 있다. 체크하고 넘어가자.
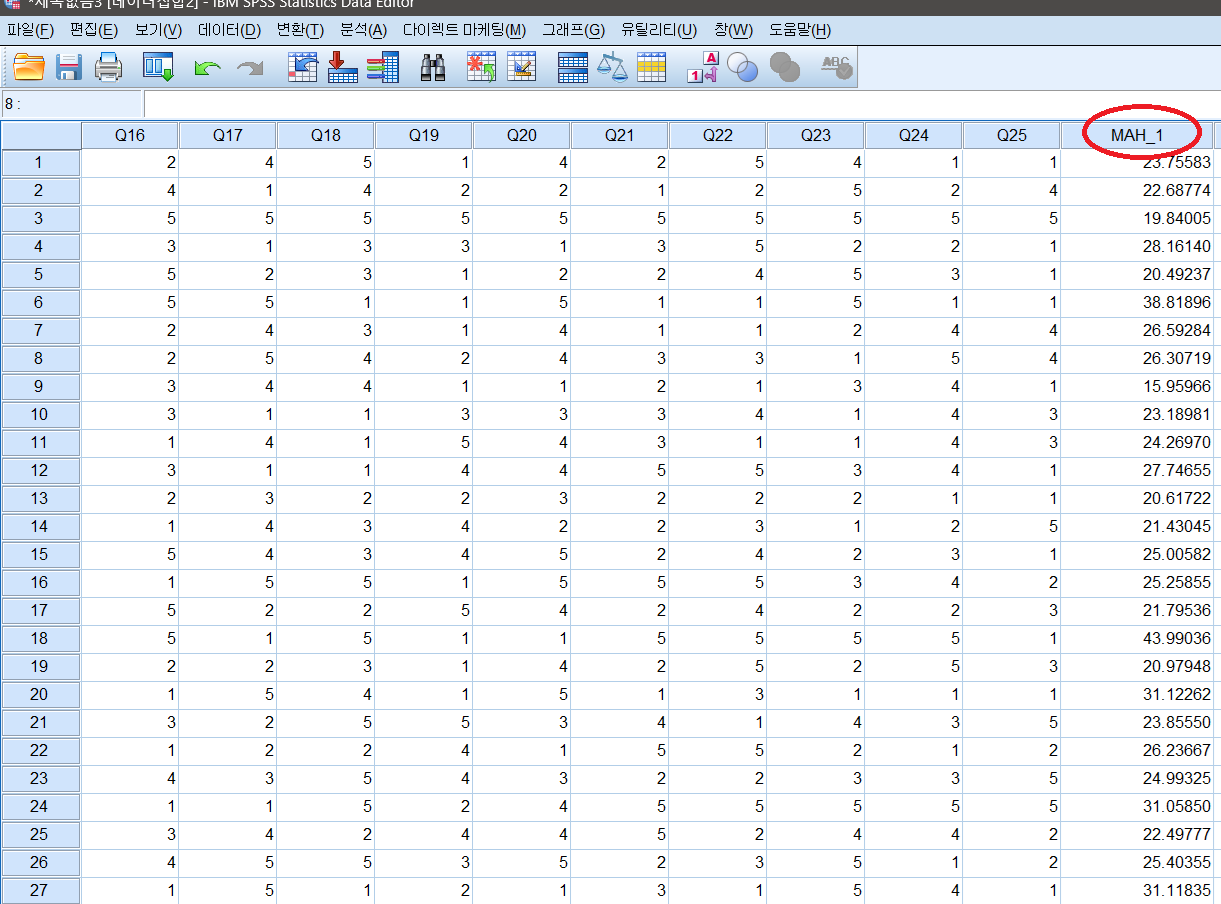
결과값 출력이 아니라, 데이터파일로 돌아가보면 MAH_1 이라는 변수가 추가된 것을 알 수 있다.
이상치를 판별하는 기준은
카이스퀘어분포표 [Moon Repeat Wiki]
jump to: Search / 사용자 도구 / Main Content / Change Content Width
www.moonrepeat.org
카이제곱 분포표에 따라 값이 달라진다. 손으로 직접 계산하기는 어렵기 때문에, 분포표를 참고하는게 편하다. 예를 들어, 이번 사례에서는 문항 수가 25개이므로 자유도(df)는 25가 된다. 따라서 분포표의 왼쪽에서 자유도 25를 찾고, 연구 목적에 맞게 적절한 유의수준(α)을 선택하면 된다. 앞서 외상 후 성장 척도 확장판(PTGI-X)의 심리측정적 속성: 한국판 척도의 요인구조와 유용성 재검토(임선영 2023) 에서는 상위 5% 백분위를 초과하는 값을 이상치로 간주했다는 것은, 연구자가 이상치를 제거할 기준을 χ²(p) 분포의 95% 백분위수로 설정한 것을 의미한다. 즉, 유의수준은 0.05이다. 카이제곱 분포표를 찾아보면 유의수준 0.05에서 df=25의 임계값은 37.65248다. 이 값을 기준으로 잡고 초과하는 값을 이상치로 간주해서 해당 응답을 소거하면 된다.

이런 식으로 말이다.

문제는 이러한 통계적 개념이 일반적인 통계학 책에서 찾아보기 힘들다. (다변량분석의 심화책에서는 볼 수 있다.) 쿡의 거리까지는 다뤄도 마할라노비스 거리에 대한 개념을 찾기가 어려웠고, 오히려 머신러닝알고리즘과 관련된 책에서 찾을 수 있었다.
+ 자유도(df)의 경우, 척도의 차원이 되어야할지 각각 독립적인 것으로 보고 문항의 개수가 자유도가 되어야할지 필자도 자세히 모른다. 아마 문항의 개수가 자유도가 되어야하는 것이 맞을듯한데.. 여
해당 예시의 데이터파일