단순회귀분석(Simple Linear Regression)

  상관계수는 두 변수 간의 선형적 관계만을 검증하는 데 그치지만, 회귀분석은 독립변수와 종속변수를 설정하여 이 둘의 인과관계를 분석하는 방법이다. 단순회귀분석은 하나의 독립변수를 다루지만, 다중회귀분석에서는 두 개 이상의 독립변수를 다룬다.  회귀분석에서 종속변수는 반드시 간격 또는 연속 척도로 측정되어야 하지만, 독립변수는 명목척도와 같은 비연속형 변수를 포함 할 수 있다. 다만, 명목척도를 사용할 경우 이를 더미변수(dummy variable)로 변환하는 과정이 필수적이다.

 

https://321fsdw.tistory.com/50

더미변수(dummy variable)란?

더미 변수에 관한 것은 이 글을 참고하면 될 것이다.

 

  단순회귀분석은 정규성, 등분산성, 독립성, 선형성을 가정한다. 이 중 선형성은 독립변수와 종속변수 간의 관계가 선형적으로 나타나야 함을 의미하며, 이는 데이터를 통해 검증해야 한다. 연구자가 연구 주제에 대해 가정을 세울 수 있지만, 데이터가 이 가정을 만족하는지 반드시 확인해야 한다.

 

 방금 이야기한 예시의 회귀분석의 귀무가설과 대립가설은 다음과 같다.

귀무가설(H₀): 우울의 정도에 따라 삶의 만족도에 영향을 미치지 않는다.
대립가설(H₁): 우울의 정도에 따라 삶의 만족도에 영향을 미칠 것이다.

 

  여기서 의문을 가질 수 있다. 상관분석과 별 다른 차이가 없는데요? 좋은 지적이다. 여기서 상관분석과 회귀분석의 중요한 결정적인 차이를 설명하고자 한다. 상관분석은 두 변인간의 어느 정도로 연결되어있을까? 에 대해 알아 보는 것이다. 즉, 독립변인으로 인해 종속변인이 이루어진다는 가정이 아니라 독립변수와 종속변수의 연결 정도를 측정하는 것이다.( X↔Y ) 다시 말해 두 변수의 관계와 강도를 측정하는, 상관관계를 알아보는데 목적이 있다.

반면에 회귀분석은, 독립변수가 종속변수에 어느 정도 영향을 미치는지 알아보는데 의의가 있다. (X → Y) 즉, 인과관계를 알아보는데 목적이 있는 것이다.

 

  쉽게 말하자면, 상관분석은 우울이 삶의 만족도에 영향을 줄 수도 있고, 삶의 만족도가 우울에 영향을 줄 수도 있다는 논리로 두 변수 간의 관계를 알아보는 데 초점이 맞춰져있지만, 회귀분석은 우울이 삶의 만족도에 영향을 준다는 명확한 원인과 결과의 관계를 측정하고자 하는 것이다.

 

spss 20에서 단순회귀분석의 절차 1

분석(A) - 회귀분석(R) - 선형(L) 을 클릭한다.

spss 20에서 단순회귀분석의 절차 2

다음과 같은 창이 뜨는데, 독립변수와 종속변수를 구분해서 잘 투입하면 된다.

spss 20에서 단순회귀분석의 절차 3

통계량(S)을 클릭하면 다음과 같은 화면과 같이 설정하면 된다. 각각 값에 대해 평균과 표준편차도 알고싶다면 기술통계(D)에 체크를 하면 될 것이다. 그 외에는 다중회귀분석이 아니면 체크할 일이 없다.

spss 20에서 단순회귀분석의 절차 4

 

  피어슨 상관계수에서는 -.982로 강한 음의 상관관계가 나타났다. 유의수준은 .00이므로 검정결과값은 유의하다 볼 수있다. 모형요약에서는 R값, R제곱, 수정된 R제곱이 있는데, 도표로 개념에 대해 설명하도록 하겠다.

R	독립변수와 종속변수 간의 상관계수	선형관계를 측정. 1에 가까울 수록 강한 선형관계를 뜻함.
R 제곱	종속변수의 변동 중, 독립변수에 의해 설명되는 비율, 회귀모델의 설명력	값이 클 수록 독립변수가 종속변수를 잘 설명한 것을 뜻함.
수정된 R 제곱	독립변수의 개수와 표본크기를 고려하여 수정된 R제곱값	독립변수가 많아지면 R제곱값이 한없이 커지기에 수정하는 절차를 거침.

 

  R은 상관계수의 값이다. 해당 분석에서는 R제곱이 .964가 나왔으므로, 삶의 만족도의 변동 중, 우울에 의해  96.4%에 의해 설명되었다고 볼 수 있다. 수정된 R제곱이 R제곱 값과 같은 이유는 해당 분석이 단순회귀분석이고, 독립변인이 하나이기 때문이다.  다중회귀분석일 경우 수정된 R제곱값이 다르다.

 

  분산분석의 결과는 회귀모형의 유의성을 평가하기 위한 것으로, 독립변수가 종속변수의 변동을 통계적으로 유의미하게 설명하는지를 판단해준다. 선형성의 유무는 잔차 분석 또는 산포도 등을 통해 별도로 검토한다.

 

다음은 선형성의 유무를 확인하기위한 산포도를 그리는 방법의 절차다.

spss 20 에서 산점도 그리기 절차 1

 

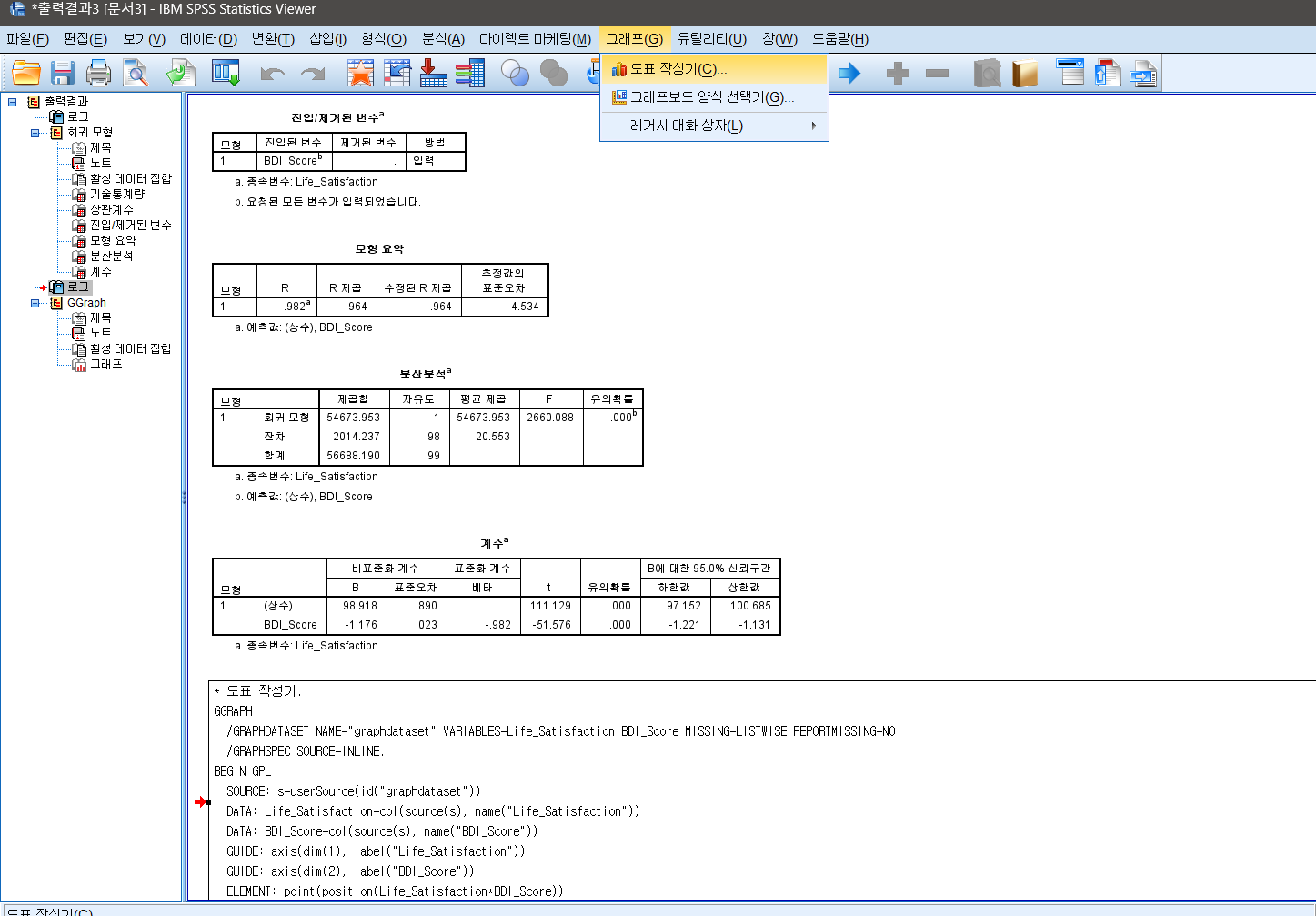
상단 메뉴의 그래프(G) - 도표작성기(C)를 클릭 

spss 20 에서 산점도 그리기 절차 2

 

X축에는 독립변인, Y축에는 종속변인을 삽입한다. 각각 우울점수와 삶의 만족도를 넣으면 된다. 그 후에 하단에서 갤러리를 클릭하고, 산점도/점도표를 클릭하고 8개 그림 중 첫 번째 그림을 위 화면의 빈 공간에 드래그한 뒤, 확인을 누른다.

spss 20 에서 산점도 그리기 절차 3

결과를 보면 우울점수가 높아질 수록, 삶의 만족도가 떨어지는 음의 상관관계를 시각화해서 볼 수 있다. 실제 연구에서는 이렇게 예쁜 그림이 안 나온다. 해당 상관계수가 -.982이기에 직선에 가까운 산포도가 나오는 것이다. 

 

 

데이터 예시파일을 첨부하오니 꼭 연습해보시길

BDI_Life_Satisfaction_Data_No_Decimals.csv

0.00MB